Estimating the Relationships Between Variables in a Spreadsheet Model Can Be Done Using:
How to Calculate Correlation Between Variables in Python
Last Updated on August 20, 2020
There may be circuitous and unknown relationships between the variables in your dataset.
Information technology is important to detect and quantify the degree to which variables in your dataset are dependent upon each other. This knowledge tin help you improve set your data to meet the expectations of machine learning algorithms, such as linear regression, whose performance will degrade with the presence of these interdependencies.
In this tutorial, you volition find that correlation is the statistical summary of the human relationship between variables and how to calculate information technology for dissimilar types variables and relationships.
Later on completing this tutorial, you will know:
- How to summate a covariance matrix to summarize the linear relationship betwixt ii or more variables.
- How to summate the Pearson's correlation coefficient to summarize the linear relationship between ii variables.
- How to calculate the Spearman'southward correlation coefficient to summarize the monotonic human relationship between two variables.
Kicking-start your project with my new book Statistics for Machine Learning, including step-by-step tutorials and the Python source code files for all examples.
Let's get started.
- Update May/2018: Updated description of the sign of the covariance (thanks Fulya).
How to Utilise Correlation to Sympathise the Relationship Betwixt Variables
Photo by Fraser Mummery, some rights reserved.
Tutorial Overview
This tutorial is divided into 5 parts; they are:
- What is Correlation?
- Test Dataset
- Covariance
- Pearson'south Correlation
- Spearman's Correlation
Need help with Statistics for Machine Learning?
Take my free seven-day email crash course now (with sample code).
Click to sign-upwards and also become a free PDF Ebook version of the course.
What is Correlation?
Variables within a dataset can be related for lots of reasons.
For instance:
- One variable could cause or depend on the values of some other variable.
- One variable could be lightly associated with some other variable.
- 2 variables could depend on a third unknown variable.
It tin be useful in data assay and modeling to better understand the relationships between variables. The statistical human relationship between two variables is referred to as their correlation.
A correlation could be positive, meaning both variables move in the aforementioned direction, or negative, meaning that when one variable's value increases, the other variables' values decrease. Correlation can also be neutral or aught, significant that the variables are unrelated.
- Positive Correlation: both variables change in the aforementioned management.
- Neutral Correlation: No human relationship in the change of the variables.
- Negative Correlation: variables change in opposite directions.
The functioning of some algorithms can deteriorate if two or more variables are tightly related, called multicollinearity. An instance is linear regression, where one of the offending correlated variables should be removed in club to improve the skill of the model.
We may too be interested in the correlation betwixt input variables with the output variable in gild provide insight into which variables may or may not be relevant as input for developing a model.
The structure of the relationship may be known, e.yard. it may be linear, or nosotros may take no thought whether a relationship exists betwixt ii variables or what construction it may accept. Depending what is known about the relationship and the distribution of the variables, unlike correlation scores can be calculated.
In this tutorial, we will look at one score for variables that take a Gaussian distribution and a linear relationship and another that does not presume a distribution and will report on any monotonic (increasing or decreasing) relationship.
Test Dataset
Before we look at correlation methods, let'southward define a dataset we can use to test the methods.
Nosotros will generate 1,000 samples of two two variables with a stiff positive correlation. The showtime variable volition be random numbers drawn from a Gaussian distribution with a mean of 100 and a standard deviation of 20. The second variable will be values from the kickoff variable with Gaussian noise added with a mean of a l and a standard deviation of 10.
We will apply the randn() office to generate random Gaussian values with a mean of 0 and a standard deviation of 1, and so multiply the results past our ain standard deviation and add together the mean to shift the values into the preferred range.
The pseudorandom number generator is seeded to ensure that we get the same sample of numbers each time the code is run.
| 1 two three 4 5 vi 7 8 9 10 11 12 thirteen 14 15 sixteen 17 | # generate related variables from numpy import hateful from numpy import std from numpy . random import randn from numpy . random import seed from matplotlib import pyplot # seed random number generator seed ( 1 ) # gear up data data1 = 20 * randn ( 1000 ) + 100 data2 = data1 + ( x * randn ( 1000 ) + 50 ) # summarize impress ( 'data1: mean=%.3f stdv=%.3f' % ( mean ( data1 ) , std ( data1 ) ) ) print ( 'data2: hateful=%.3f stdv=%.3f' % ( mean ( data2 ) , std ( data2 ) ) ) # plot pyplot . scatter ( data1 , data2 ) pyplot . prove ( ) |
Running the case first prints the hateful and standard deviation for each variable.
| data1: mean=100.776 stdv=19.620 data2: mean=151.050 stdv=22.358 |
A scatter plot of the two variables is created. Because we contrived the dataset, we know in that location is a human relationship between the two variables. This is articulate when we review the generated besprinkle plot where nosotros can see an increasing tendency.
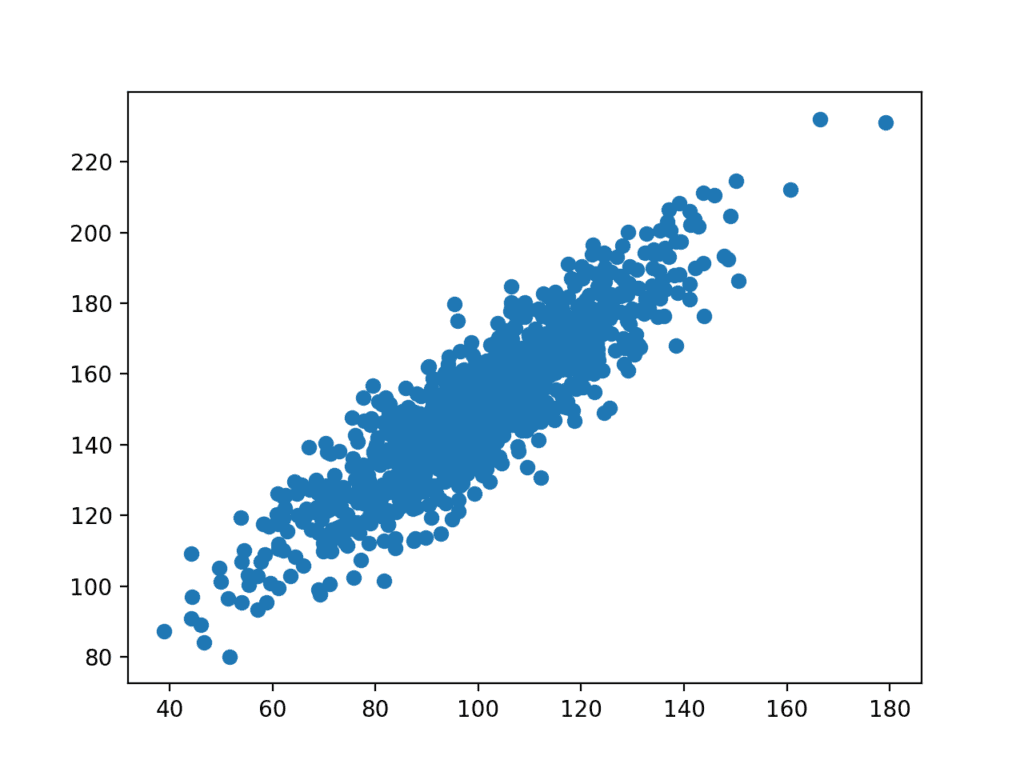
Besprinkle plot of the test correlation dataset
Before we await at calculating some correlation scores, we must first look at an important statistical building cake, chosen covariance.
Covariance
Variables tin be related by a linear relationship. This is a relationship that is consistently condiment beyond the 2 data samples.
This human relationship can be summarized between two variables, called the covariance. It is calculated every bit the average of the production betwixt the values from each sample, where the values haven been centered (had their hateful subtracted).
The calculation of the sample covariance is equally follows:
| cov(X, Y) = (sum (x - mean(Ten)) * (y - mean(Y)) ) * 1/(northward-1) |
The apply of the hateful in the calculation suggests the need for each data sample to take a Gaussian or Gaussian-like distribution.
The sign of the covariance can be interpreted every bit whether the ii variables change in the aforementioned direction (positive) or change in different directions (negative). The magnitude of the covariance is not easily interpreted. A covariance value of zero indicates that both variables are completely independent.
The cov() NumPy function tin be used to calculate a covariance matrix between ii or more than variables.
| covariance = cov ( data1 , data2 ) |
The diagonal of the matrix contains the covariance between each variable and itself. The other values in the matrix represent the covariance between the ii variables; in this case, the remaining two values are the same given that nosotros are computing the covariance for only 2 variables.
Nosotros can calculate the covariance matrix for the two variables in our test problem.
The complete example is listed below.
| # summate the covariance betwixt ii variables from numpy . random import randn from numpy . random import seed from numpy import cov # seed random number generator seed ( ane ) # fix data data1 = xx * randn ( thousand ) + 100 data2 = data1 + ( 10 * randn ( grand ) + 50 ) # summate covariance matrix covariance = cov ( data1 , data2 ) impress ( covariance ) |
The covariance and covariance matrix are used widely within statistics and multivariate analysis to characterize the relationships betwixt two or more variables.
Running the example calculates and prints the covariance matrix.
Because the dataset was contrived with each variable drawn from a Gaussian distribution and the variables linearly correlated, covariance is a reasonable method for describing the relationship.
The covariance between the two variables is 389.75. We tin come across that it is positive, suggesting the variables change in the same direction as nosotros look.
| [[385.33297729 389.7545618 ] [389.7545618 500.38006058]] |
A problem with covariance as a statistical tool alone is that information technology is challenging to interpret. This leads us to the Pearson's correlation coefficient next.
Pearson's Correlation
The Pearson correlation coefficient (named for Karl Pearson) tin can be used to summarize the force of the linear relationship between two information samples.
The Pearson'due south correlation coefficient is calculated as the covariance of the two variables divided by the product of the standard deviation of each information sample. It is the normalization of the covariance betwixt the two variables to give an interpretable score.
| Pearson's correlation coefficient = covariance(10, Y) / (stdv(X) * stdv(Y)) |
The use of mean and standard departure in the calculation suggests the need for the two data samples to have a Gaussian or Gaussian-like distribution.
The effect of the adding, the correlation coefficient can be interpreted to sympathise the relationship.
The coefficient returns a value between -1 and one that represents the limits of correlation from a full negative correlation to a full positive correlation. A value of 0 means no correlation. The value must exist interpreted, where oftentimes a value below -0.five or above 0.5 indicates a notable correlation, and values below those values suggests a less notable correlation.
The pearsonr() SciPy function can be used to summate the Pearson'southward correlation coefficient between two data samples with the aforementioned length.
We tin calculate the correlation betwixt the two variables in our exam problem.
The complete example is listed below.
| # summate the Pearson's correlation between two variables from numpy . random import randn from numpy . random import seed from scipy . stats import pearsonr # seed random number generator seed ( 1 ) # prepare information data1 = xx * randn ( g ) + 100 data2 = data1 + ( 10 * randn ( 1000 ) + 50 ) # calculate Pearson's correlation corr , _ = pearsonr ( data1 , data2 ) print ( 'Pearsons correlation: %.3f' % corr ) |
Running the instance calculates and prints the Pearson's correlation coefficient.
We can see that the ii variables are positively correlated and that the correlation is 0.8. This suggests a high level of correlation, e.g. a value in a higher place 0.5 and close to 1.0.
| Pearsons correlation: 0.888 |
The Pearson'due south correlation coefficient can exist used to evaluate the human relationship betwixt more than two variables.
This tin can be done by calculating a matrix of the relationships betwixt each pair of variables in the dataset. The consequence is a symmetric matrix called a correlation matrix with a value of one.0 along the diagonal as each column ever perfectly correlates with itself.
Spearman's Correlation
Two variables may exist related past a nonlinear relationship, such that the human relationship is stronger or weaker across the distribution of the variables.
Further, the two variables existence considered may have a not-Gaussian distribution.
In this instance, the Spearman'southward correlation coefficient (named for Charles Spearman) can be used to summarize the force between the two information samples. This test of human relationship tin also be used if there is a linear relationship betwixt the variables, just volition have slightly less power (e.grand. may result in lower coefficient scores).
As with the Pearson correlation coefficient, the scores are between -1 and one for perfectly negatively correlated variables and perfectly positively correlated respectively.
Instead of computing the coefficient using covariance and standard deviations on the samples themselves, these statistics are calculated from the relative rank of values on each sample. This is a mutual approach used in non-parametric statistics, e.g. statistical methods where we practice not assume a distribution of the information such as Gaussian.
| Spearman's correlation coefficient = covariance(rank(Ten), rank(Y)) / (stdv(rank(X)) * stdv(rank(Y))) |
A linear human relationship between the variables is non assumed, although a monotonic human relationship is assumed. This is a mathematical proper name for an increasing or decreasing relationship between the two variables.
If yous are unsure of the distribution and possible relationships between two variables, Spearman correlation coefficient is a good tool to employ.
The spearmanr() SciPy role can be used to calculate the Spearman'southward correlation coefficient between 2 data samples with the same length.
We tin calculate the correlation between the 2 variables in our exam problem.
The consummate example is listed below.
| # calculate the spearmans's correlation between two variables from numpy . random import randn from numpy . random import seed from scipy . stats import spearmanr # seed random number generator seed ( 1 ) # set up data data1 = twenty * randn ( 1000 ) + 100 data2 = data1 + ( 10 * randn ( 1000 ) + 50 ) # calculate spearman's correlation corr , _ = spearmanr ( data1 , data2 ) print ( 'Spearmans correlation: %.3f' % corr ) |
Running the case calculates and prints the Spearman'south correlation coefficient.
We know that the data is Gaussian and that the relationship betwixt the variables is linear. All the same, the nonparametric rank-based arroyo shows a strong correlation between the variables of 0.8.
| Spearmans correlation: 0.872 |
As with the Pearson's correlation coefficient, the coefficient tin be calculated pair-wise for each variable in a dataset to give a correlation matrix for review.
For more help with not-parametric correlation methods in Python, see:
- How to Calculate Nonparametric Rank Correlation in Python
Extensions
This department lists some ideas for extending the tutorial that you may wish to explore.
- Generate your own datasets with positive and negative relationships and calculate both correlation coefficients.
- Write functions to calculate Pearson or Spearman correlation matrices for a provided dataset.
- Load a standard auto learning dataset and calculate correlation coefficients between all pairs of real-valued variables.
If you explore any of these extensions, I'd dearest to know.
Further Reading
This section provides more resources on the topic if you are looking to get deeper.
Posts
- A Gentle Introduction to Expected Value, Variance, and Covariance with NumPy
- A Gentle Introduction to Autocorrelation and Partial Autocorrelation
API
- numpy.random.seed() API
- numpy.random.randn() API
- numpy.mean() API
- numpy.std() API
- matplotlib.pyplot.scatter() API
- numpy.cov() API
- scipy.stats.pearsonr() API
- scipy.stats.spearmanr() API
Manufactures
- Correlation and dependence on Wikipedia
- Covariance on Wikipedia
- Pearson correlation coefficient on Wikipedia
- Spearman'south rank correlation coefficient on Wikipedia
- Ranking on Wikipedia
Summary
In this tutorial, y'all discovered that correlation is the statistical summary of the relationship between variables and how to calculate information technology for different types variables and relationships.
Specifically, you learned:
- How to summate a covariance matrix to summarize the linear relationship between ii or more variables.
- How to summate the Pearson'south correlation coefficient to summarize the linear human relationship between two variables.
- How to calculate the Spearman's correlation coefficient to summarize the monotonic relationship between two variables.
Exercise you lot have any questions?
Ask your questions in the comments below and I will do my best to reply.
Become a Handle on Statistics for Machine Learning!
Develop a working understanding of statistics
...past writing lines of lawmaking in python
Detect how in my new Ebook:
Statistical Methods for Machine Learning
It provides self-study tutorials on topics similar:
Hypothesis Tests, Correlation, Nonparametric Stats, Resampling, and much more...
Detect how to Transform Data into Noesis
Skip the Academics. Just Results.
See What's Inside
Source: https://machinelearningmastery.com/how-to-use-correlation-to-understand-the-relationship-between-variables/
0 Response to "Estimating the Relationships Between Variables in a Spreadsheet Model Can Be Done Using:"
Postar um comentário